001
// Operating Greedy
int marker = 0;
for (int i = N-1; i >= 0; i--) {
if (K >= F[i])
marker += K / F[i];
K = K % F[i];
}전체 값이 있고, 변동되는 plate를 사용할 때,
- plate로 나눈 몫은 plate 사용 횟수이고
- plate로 나눈 나머지는, 다음 plate 사용을 위한 것
-
002
// L2~
PriorityQueue<Integer> pQ = new PriorityQueue<>();
for (int i = 0; i < N; i++) {
int cont = sc.nextInt();
pQ.add(cont);
}- container는 인식자이다
-
003
// Operating Comparison
int plate = 0;
while (pq.size() != 1) {
int d1 = pq.remove();
int d2 = pq.remove();
plate += d1 + d2;
pq.add(d1 + d2);
}
// OEC
System.out.println(plate);- 2개 처리하면 1개가 생김, 즉 1씩 줄어드는 것이고, 마지막에 무조건 1개가 남음
- 그 1개는 Queue에 생기는 것이지만 신경쓰지 말고, 이미 plate에 축적 보존된 값만 출력하면 됨
-
004
// L2~
PriorityQueue<Integer> plusPq = new PriorityQueue<>(Collections.reverseOrder());
PriorityQueue<Integer> minusPq = new PriorityQueue<>();
int oneMarker = 0;
int zeroMarker = 0;
for (int i = 0; i < N; i++) {
int data = sc.nextInt();
if (data > 1) {
plusPq.add(data);
} else if (data == 1) {
oneMarker++;
} else if (data == 0) {
zeroMarker++;
} else {
minusPq.add(data);
}
}plusPq로 받고 반전정렬 추가
minusPq는 절댓값이 큰 게 작은거니 추가정렬 할 필요 없음
1은 곱해봤자 1이 상실되므로, 그냥 더하는게 맞음
0은 있으면 남은 음수랑 곱할 수 있으니 숫자만 중요
-
005
// Operation plus
int plate = 0;
while (plusPq.size() > 1) {
int s = plusPq.remove();
int e = plusPq.remove();
plate += s + e;
}
if (!plusPq.isEmpty()) {
plate += plusPq.remove();
}
// Operation minus
while (minusPq.size() > 1) {
int s = minusPq.remove();
int e = minusPq.remove();
plate += s * e;
}
if (!minusPq.isEmpty()) {
if (zeroMarker == 0)
plate += minusPq.remove();
}plate는 하나로 계속 사용하면 됨
마지막 minus값은 (-) 이므로 뺴는게 아닌 더하는게 맞음
-
006
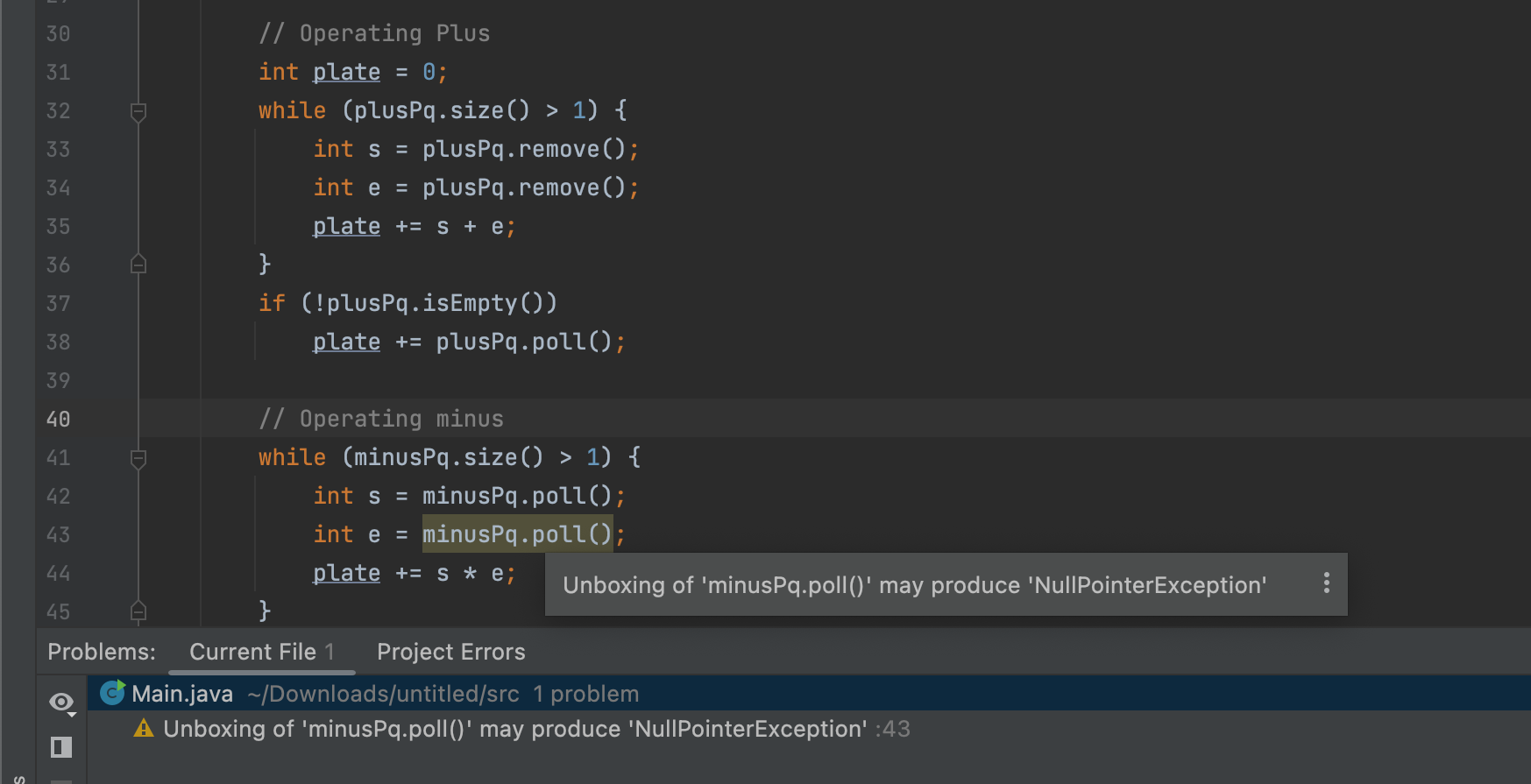
Queue에서 remove 대신 poll로 사용하면 안됨
마지막 남은 minus를 없애기
- zero는 있기만 하면 됨
- 즉 if phaser의 한쪽이 나머지 한쪽을 커버하므로
- zero가 없는 상태만 서술해주면 됨
while(!pQ.isEmpty()) 로 바로 사용하지 않고
- 두개씩 쌍을 지어 없애고, 마지막 남은 하나를 없애야 하는데
- 2개가 남은 경우 > while()에 걸려들고 남는것이 없어져 정리 완료
- 1개가 남은 경우 > while에서 Outflux되고 if에 걸려서 정리 완료
- 3개가 남은 경우 > while에 걸려들고 남은 1개는 아래 if에 걸려듬
-
007
// L2 ~
int[][] F = new int[C][2];
for (int i = 0; i < C; i++) {
F[i][0] = sc.nextInt();
F[i][1] = sc.nextInt();
}- ArrayList가 아닌, 이차원 배열로 값을 받는다
-
008
//PRe
Arrays.sort(F, new Comparator<int[]>() {
@Override
public int compare(int[] S, int[] E) {
if (S[1] == E[1]) {
return S[0] - E[0];
}
return S[1] - E[1];
}
});- 끝나는 시간 같을 때, 시작 시간이 일찍인 순으로 정렬하고
- 나머지는 끝나는 시간이 일찍인 순으로 정렬
-
009
// Greedy
int marker = 0;
int end = -1;
for (int i = 0; i < C; i++) {
if (F[i][0] >= end) {
end = F[i][1];
marker++;
}
}겹치지 않을 떄
F 첫 인자는 무조건 end = -1보다 크다
-
010
// ISC - L1
Scanner sc = new Scanner(System.in);
String example = sc.nextLine();
String[] str = example.split("-");> String 받아서 - 부호 기준으로 쪼개기
-
011
// EM : calculator
static int mySum(String a) {
int plate = 0;
String[] temp = a.split("[+]");
for (int i = 0; i < temp.length; i++) {
plate += Integer.parseInt(temp[i]);
}
return plate;
}마이너스 기준으로 쪼개진 걸
합쳐서 다시 리턴해줌
-
012
// Operating Greedy
for (int i = 0; i < str.length; i++) {
int temp = mySum(str[i]);
if (i == 0)
answer += temp;
else
answer -= temp;
}첫번째 +는 더하고, 나머지는 다 마이너스
-
013
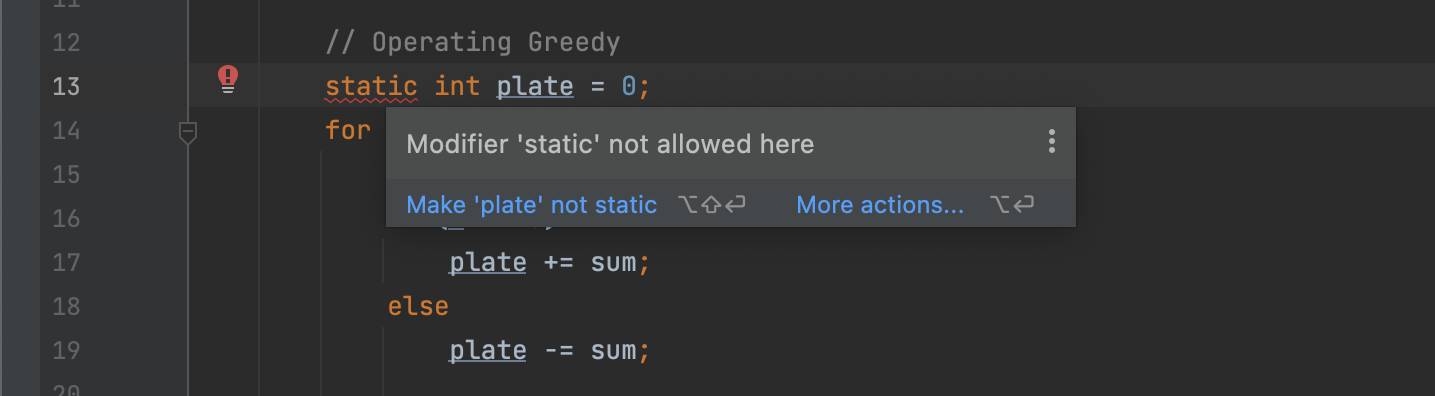
class 내 public static void main{} 공간에서는 static 사용 불가
-
014
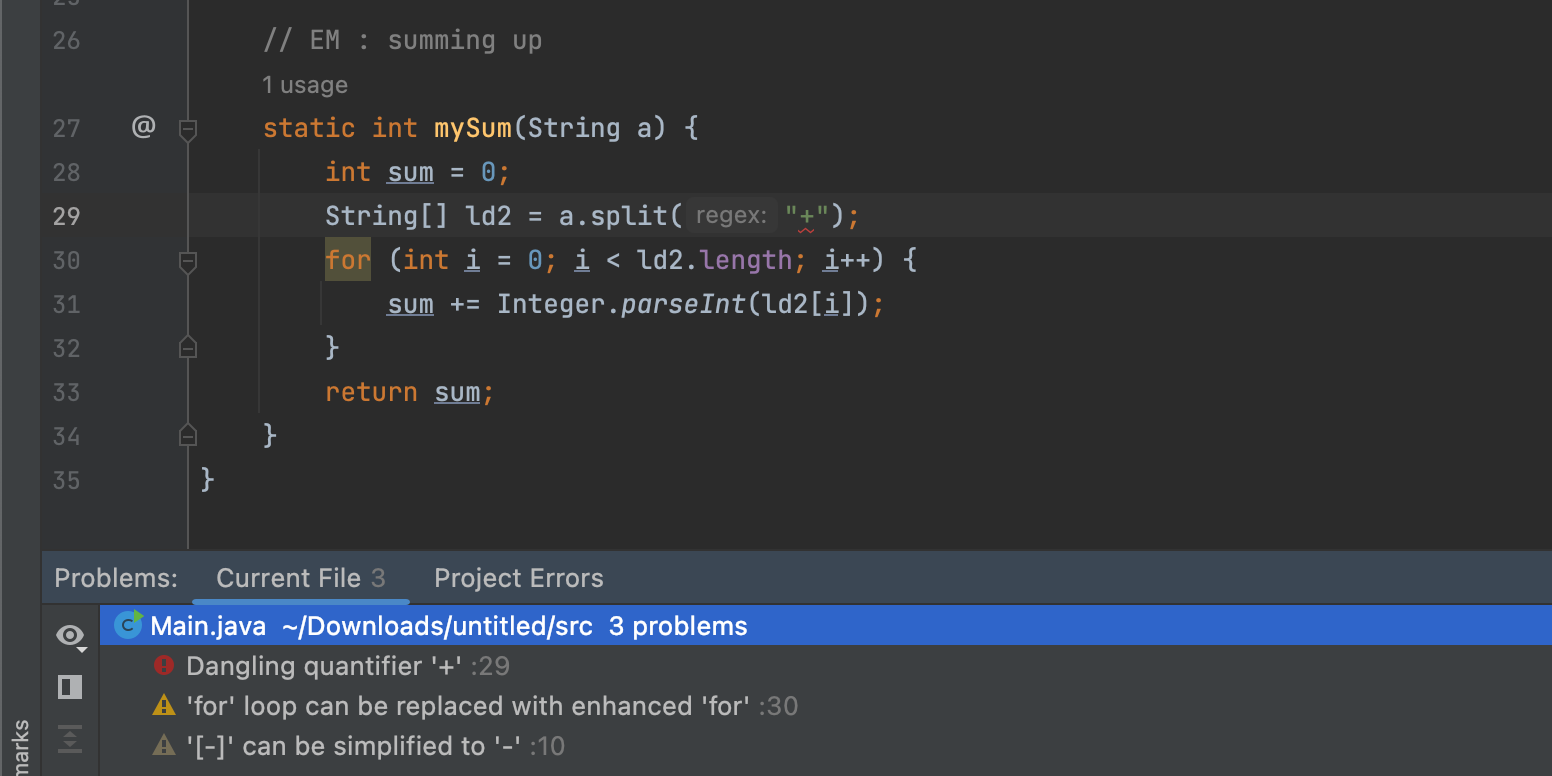
메인 공간에서의 - 기준 split은 []로 안 감싸도 되지만
외부 모듈 공간에서의 + 기준 split은 [] 감싸지 않으면 안 됨
> 공간 차이가 아닌 부호 자체의 문제일수도 있음
-
015
// External Module : summing up
static int sumUp(String a) {
int plate = 0;
String[] ld2 = a.split("[+]");
for (int i = 0; i < ld2.length; i++) {
plate += Integer.parseInt(ld2[i]);
}
return plate;
}
}이 plate는 해당 위상 공간에서만 쓰이는 것이므로, 다른 공간에서는 더 이상 인식되지 않는다
쓰고 잊어버리는 것
> Integer Wrapping 주의
-
016
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// ISC - L1
Scanner sc = new Scanner(System.in);
String line = sc.nextLine();
String[] ld1 = line.split("-");
// Operating Greedy
int plate = 0;
for (int i = 0; i < ld1.length; i++) {
int sum = mySum(ld1[i]);
if (i == 0)
plate += sum;
else
plate -= sum;
}
// OEC
System.out.println(plate);
}
// EM : summing up
static int mySum(String a) {
int sum = 0;
String[] ld2 = a.split("[+]");
for (int i = 0; i < ld2.length; i++) {
sum += Integer.parseInt(ld2[i]);
}
return sum;
}
}line > line depth 1 > line depth 2
로 container 구분하면 편함
'코테 기초' 카테고리의 다른 글
| 이차원 리스트 접근 (0) | 2023.07.03 |
|---|---|
| Number Theory (0) | 2022.12.20 |
| Search (0) | 2022.12.16 |
| Sort (1) | 2022.12.16 |
| 자료구조 재방문 (0) | 2022.12.16 |